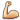Ouroboros نوشته: من یک پرسشی مطرح کردم و بحثی پیرامون آن شکل گرفتم، بد نیست اکنون که بازگشتهاید اگر فرصت کردید نظر خود را دربارهی آن بگویید: اینجا
چشم.
Ouroboros نوشته: میدانم به موضوع آن جستار(تاریخ ریاضیات)پیوندی ندارد پس اینجا میگویم. من یک سوالی دارم که خجالت میکشم آنرا مطرح بکنم، وانگهی اکنون سالهاست که با آن دست و پنجه نرم کردهام.. اینست که تا داریوش گرامی نرفتهاند ریسک میکنم و آنرا میپرسم، امیدوارم زیادی ضایع نباشد:
آیا 2xn∑ از (n برابر با صفر) تا (n برابر با بینهایت) مساویست با -1؟ و اگر بله، چرا؟ من هرچه این صفحه را زیر و زبر میکنم چیزی نمیفهمم...
خواهش میکنم امیر جان، ما بیش از اینها از شما آموختهایم، خرسند خواهم شد جایی ، به طریقی آنها را پس دهم.
همانطورکه بانو آلیس توضیح دادند این سریای که شما به آن اشاره میکنید مقدارش غیرقابل محاسبه است چون واگراست (به سوی بینهایت میل میکند). این کاملا واضح و مبرهن است و هرگز حاصل این سری -1 نخواهد شد. علاوه بر توضیحاتی که آلیس داد و آن مقالههایی که گفتید ، نکتهای که باید در نظر داشته باشید این است که استفاده از اعمالِ جبری همیشه دقیق نیستند و همیشه ما را به پاسخِ صحیح نمیرسانند! این ادعایی شگفتآور است اما حقیقت دارد. به مثالِ سادهی زیر دقت کنید:
میدانیم که
-12=-12
-> [TABLE]
[TR]
[TD]
![[عکس: 7.gif]](http://www.daftarche.com/images/imported/2013/05/7.gif)
[/TD]
[/TR]
[/TABLE]
اکنون میتوانیم به دو طرف تساوی یک عدد را اضافه کنیم:
-> [TABLE]
[TR]
[TD]
![[عکس: 8.gif]](http://www.daftarche.com/images/imported/2013/05/8.gif)
[/TD]
[/TR]
[/TABLE]
->
[TABLE]
[TR]
[TD]
![[عکس: 9.gif]](http://www.daftarche.com/images/imported/2013/05/9.gif)
[/TD]
[/TR]
[/TABLE]
اکنون دو طرف تساوی را بصورت اتحاد دوجملهای مینویسیم:
-> [TABLE]
[TR]
[TD]
![[عکس: 10.gif]](http://www.daftarche.com/images/imported/2013/05/10.gif)
[/TD]
[/TR]
[/TABLE]
اکنون از دو طرف تساوی جذر میگیریم :
-> 3-7/2=4-7/2
اکنون از دو طرفِ تساوی 7/2 را کم میکنیم:
-> 4=3
؟!
این رابطه از لحاظِ اصولِ ریاضی هیچ ایرادی ندارد. پیش هر ریاضیدانی هم که ببرید ایرادی نمیتواند از آن بگیرد.
اما اشکالی وجود دارد در این جا. استدلالِ ریاضیاتی ما ایرادی ندارد، ایراد از خود بیان ریاضی ما است. اگرچه به نظر میرسد ابزارهای ریاضیاتی بسیار دقیق هستند، اما در واقع اینطور نیست. ابزارها و سمبلهایی که ما برای بیانِ عبارات و اعمال ریاضیاتی برگزیدهایم، دقیقا منطبق بر آنچه که باید باشند نیستند. این مشکل زمانی حاد میشود که شما بخواهید از این ابزارها در شاخههای مختلف ریاضی استفاده کنید که قبلا در آن شاخهها ، کاربردشان و حدودشان پیشبینی نشده بود. چنین میشود که گاه به نتایجی اینچنین شگفتآور میرسیم. و به همین سبب است که ریاضیدانها( همچون آبل) به کلی با چنین روشهایی مخالف هستند و تنها راهِ درست را در استفاده از اصولِ اساسی آنالیزِ ریاضی با تعیین دقیق حدودِ ابزارهای بیان و متدهای محاسباتی برای اثباتها میدانند.در موردِ سریها و حسابِ بینهایتها این موضوع خیلی جدی است. و این کارهای خنک معمولا از مهندسانِ ریاضیدان سر میزند که ریاضیدانها همیشه از آنها متنفرند! نامِ کسی که این اصل را بنا نهاد به خاطر ندارم اما یکی از ریاضیدانان قرنِ نوزدهم بود به نظرم که گفت : برای اثبات یک موجودیت در یک دستگاه، به دستگاهی قویتر از آن نیاز داریم. او با مثالهای متعددی که در بالا یکی از آنها را آوردم، نشان داد که این همه اعتمادی که ما به ریاضیات داریم بیخود است! از آنجا که ریاضیات قویترین دستگاهیست که اکنون در اختیار داریم، بنابراین برای راستیآزمایی نتایج برآمده از آن ابزار دیگری در دست نیست!
از طرفی مهندسان توانِ خود را مواقعی دیگر بر سر ریاضیدانها میکوبند. این معادله را ببینید :
lnx/x =ln2/2
(ln همان لگاریتم برپایه e است).
هرگز نیمتوانید (یا به سختی بتوانید)با استفاده از جبر و روشهای گوناگونِ ریاضیاتی این معادله را حل کنید. اما کافیست به جای x چهار بگذارید!
پ.ن: این عدمِ علاقه یا تعاملِ شما با مزداهیک برای من قدری شگفتآور بود. (درست است؟)
 .
.


![[-]](https://daftarche.com/images/bootbb/collapse.png)



![[عکس: 1.gif]](http://www.daftarche.com/images/imported/2013/04/1.gif)
![[عکس: 7.gif]](http://www.daftarche.com/images/imported/2013/05/7.gif) [/TD]
[/TD]![[عکس: 8.gif]](http://www.daftarche.com/images/imported/2013/05/8.gif) [/TD]
[/TD]![[عکس: 9.gif]](http://www.daftarche.com/images/imported/2013/05/9.gif) [/TD]
[/TD]![[عکس: 10.gif]](http://www.daftarche.com/images/imported/2013/05/10.gif)